Drunkard’s Walk

Every now and then when I am doing errands, I stop at the local bookstore to see what’s new. I freely admit that I judge a book by its cover – the title, the graphics and any blurbs. I also like to stroke the cover – a nice grainy feel may be the tipping point to a purchase. The particular book that recently caught my eye was “The Drunkard’s Walk: How Randomness Rules Our Lives.” The dust jacket was very cute, consisting of punched out holes spelling out the word random. The title resonated since I have often marveled at how coincidences can change your life on a dime. (See prior fanagram, “That Moment in Time.”) Certainly my life changed for the better in 1978 when I randomly met my husband Nick at a large Christmas party that neither of us was invited to.

Stephen Hawking’s blurb on the cover said, “A wonderfully readable guide to how the laws of randomness affect our lives.” The word “law” and “randomness” would seem to be an oxymoron, but then I remembered what various Human Resources departments insisted on every time there was a reorganization, “The only constant is change,” or “Expect the Unexpected,” so I decided to buy the book. The author, Leonard Mlodinow, starts with the premise that our brains are not equipped to process long term probabilities and risk. Back when our ancestors first stood up and opposed their thumbs, there was no evolutionary pressure to think in the long term. Survival was a day-to-day battle and resources appeared endless. Our brains are just not hard-wired to understand the current long term probabilities and risk when considering such issues as IRAs or long term care insurance.

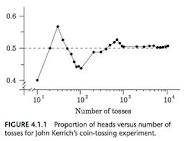
A frequent example of randomness is the simple flipping of a coin and tallying the number of head and tails. I think that we all intuitively know that each flip has a 50-50 chance of coming up heads, and that the result of one flip does not impact the result of the next flip. But we cannot help thinking that after 5 straight heads, we are “due” for a tails. It is that type of thinking that gets gamblers into trouble – it is so tempting to bet on someone who is on a “hot streak,” or conversely someone on a cold streak who is “due.” But even if there is an occasional hot streak of heads, in the long run over multiple flips, the number of heads and tails eventually approximate 50:50. John Kerrich was an unfortunate mathematician who spent almost the entirety of WWII in a German prisoner camp. He put his enforced idle time to good use by flipping a coin over and over and recording head or tails. After 100 attempts, he had 44 heads (i.e. tails seemed to be on a hot streak), but after 10,000 flips the percentage of heads (50.67%) had more closely approximated the expected 50%.

Kerrich is illustrating the law of large numbers, the revolutionary concept introduced by Bernoulli in 1713, i.e. that over a large number of observations, the incidence of random events – like flipping a coin – will become stable. The law of large numbers was one of the foundations of probability theory and is the basis of the pay outs of casinos and life insurance, which are based on multiple observations over large populations. However, We the People don’t have that wealth of information, and we are more likely to fall victim to the gambler’s fallacy, basing our decisions on single events and personal tolerance for risk. At Vegas, are we optimistic, on a hot streak or “due” for winning, or are we just wearing our lucky socks?

Flipping coins is pretty straightforward, but Mlodinow goes on to the knottier problem of the probability of extraordinary events, such as Roger Maris’s remarkable home run record in 1961, tying Babe Ruth’s longstanding record of sixty one. In previous years Maris had never hit more than 37 home runs and his batting average was around .270. Some people believe that Maris should be inducted into the Hall of Fame, based on this single year alone. However, Mlodinow points out that based on random flukes alone it is not surprising that some batter – not necessarily Maris – has a freakishly good year, i.e. somebody is going to be an outlier. Looking at this from a probability view point, the question should not be why Maris had such a good year, but rather the high probability that of all the batters in baseball since Ruth, one would have an outlier year. It just happened to be Maris, and the following year he returned to his typical 30 home runs. So here’s another tip – if you are on the upside of an outlier, take advantage of it, renegotiate your contract, get endorsements, because the opportunity may be gone by the next year. Although Maris’ salary was on a paltry $42,000, he did manage to cash in on an endorsement for Camel cigarettes.

Maris’ experience illustrates the concept of “regression to the mean,” i.e. that an exceptionally good year or bad year will be followed by a more normal year. After a disastrous game, a coach might give an impassioned locker room speech, hoping to fire up his team for the next game. When his team does indeed win the next game, he might hitch up his pants, jauntily strut out of the locker room and smugly say to himself, “Boy am I a great coach and motivator, I really gave them the old ‘win one for the Gipper’ speech in the locker room.” In actuality his team’s follow up success might be solely due to the regression to the mean. Similarly, a coach should not beat himself up if his lofty praises after a good game are followed by a team’s poor performance. It’s just regression to the mean. In the stock market, are we patient enough to wait out the random fluctuations, do we believe that an analyst’s breakout year means continued good performance, and why didn’t anyone realize that Madoff’s success was such an outlier that it confounded the laws of probability?

While the Maris story is nice, the example that I like better occurred in spring training in 2001 when the Arizona Diamondbacks played the San Francisco Giants. Randy Johnson, aka the “Big Unit,” reared back to hurl one of his signature 95 MPH fast balls. Unbelievably, he nailed a pigeon that just happened to be flying by. The video shows an explosion of white features, drifting into a fluffy mound like oversized snow flakes, and a denuded (and dead) bird falling a couple of feet near by along the first base line. Everyone that I know who has seen the video has erupted in laughter, due to the fate of the poor pigeon and the total improbability of the incident. I remember seeing the clip as a sports show highlight, where the announcers had to stifle their laughter in deference to the dead pigeon and the back lash from animal rights advocates.

The immediate question was the probability that Randy Johnson would hit a pigeon. The more relevant probability is the chance that some pitcher, sometime in the entire history of recorded baseball, would nail a pigeon. Mathematicians rose to the challenge and calculated the number of pitches that have been thrown in all of professional baseball games, the radius and velocity of the baseball and the size, number and velocity of birds flying around a stadium and concluded that the chances of ball meeting bird were actually pretty good. (Incidentally, this type of calculation sounds like it can be used to determine the probability of the earth being decimated, dinosaur style, i.e. Randy Johnson = asteroid and our sweet earth = pigeon.) Skeptics pointed that while there may be a lot of birds in a stadium, most of them are not flying in front of home plate, but instead making their living eating old hot dog buns and popcorn. The mathematician conceded that the number of pigeons was based on an observational guesswork, but that even if he was off by a factor of 100, there was still a reasonable chance. So while the probability that a pitched ball hitting a bird may be relatively high, the randomness is that the pitcher happened to be the fearsome Randy Johnson, with the added twist that he was perfect pitcher to demolish a bird.

There are many internet videos of birds being hit in other games – golf, tennis and soccer among them. Nick can contribute to the randomness of being one of those people who has offed a bird. He plays golf about once every five years, and hits a drive like a hockey slap shot, his preferred sport. About 20 years ago, he was playing with his stepfather on a par three course, where his strategy was to give his tee shot a mighty whack in the hopes that he would at least partially connect. He was initially excited when one drive really took off and cleared the water hazard (actually a sewage canal), but was immediately dismayed to realize that he had overshot the green by at least 50 yards. And then an attack of randomness. The soaring ball hit a robin and both abruptly plummeted to the green. The bird was dead, and for the first and only time in his life, Nick putted out and got a “birdie.” For years I did not believe this story, thinking it too improbable to be true. But now it makes sense, in the big scheme of things the event was predictable, and the only randomness was that Nick was the golfer.

The subtitle of the book, “How Randomness Rules Our Lives” is somewhat intimidating. We struggle to create a safe path, but are we all just in a drunkard’s walk, lurching crazily from one random event to another, succumbing to the gambler’s fallacy, nailing birds and dodging bullets? The bulk of my day may be random events, but most are nothing more than trivial white noise. Others are comical, some are painful (last week I randomly stepped on a tennis ball and sprained my ankle), some are unspeakably tragic, and some are beautiful and without them life would be a dreary bore. I am sitting looking out the window as the sun sets. The trees across the prairie are already blue black, but strips of deep red and pale yellow of the disappearing sun peek through, interrupted by the indigo blue of clouds. Silhouettes of ducks fly overhead, and a bicyclist passes on the path. Randomly beautiful. And then in the midst of a drunken walk there is random joy. To wit: December, 1978, Chris Nielson’s birthday party, in a seething throng of people, I just happened to be standing next to Nick.